
La duration e la duration modificata sono due indicatori importanti del rischio di un bond che devi conoscere. Altrimenti continuerai a sbagliare strategia.
La duration di un titolo
La durata media finanziaria, nota come duration, è un indicatore della rischiosità di un titolo obbligazionario. In breve essa misura la maggiore o minore reattività della quotazione di un bond rispetto alle variazioni dei tassi di interesse. Prima di vedere come si calcola la duration, fermiamoci un attimo a comprenderne le variabili che la influenzano.
Basta errori. Fai sul serio con i tuoi investimenti facendo le poche cose che fanno realmente la differenza. Inizia da qui.
Durata del titolo
Il fattore più importante nel calcolo della duration è la vita residua del bond. Al crescere della stessa, infatti, cresce anche la duration finanziaria.
Cedola
La cedola di un’obbligazione ha, invece, un impatto inverso sulla duration e quindi sulla rischiosità. Tanto più essa è alta, tanto minore sarà la durata media finanziaria del titolo e viceversa. A titolo di esempio gli zero coupon, che sono privi di cedole periodiche, hanno una duration uguale alla vita residua.
Prezzo delle obbligazioni
Per quanto riguarda la quotazione dei bond, tra loro e la duration esiste una relazione inversa. In altri termini, a parità di rendimento effettivo i titoli che presentano quotazioni più alte hanno di solito una duration inferiore.
Tasso di interesse
In modo analogo al precedente, il tasso di interesse ha una influenza negativa sulla duration finanziaria. Intendo dire che un rialzo dei tassi di rendimento comporta una riduzione dell’indicatore.
Formula di calcolo
La formula della duration è abbastanza complessa. In particolare essa prevede che si eseguano i seguenti passaggi:
- calcolo del rendimento effettivo netto dell’obbligazione
- attualizzazione, con la formula dell’interesse composto, delle cedole e del capitale a scadenze
- moltiplicazione del dato precedente per il tempo che manca alla scadenza dei singoli pagamenti
- somma dei prodotti ottenuti al punto precedente
- divisione della somma per il prezzo tel quel del bond, ossia la quotazione comprensiva del rateo di interessi.
Per chi è interessato ad approfondire, ecco la formula di matematica finanziaria per il calcolo della duration:
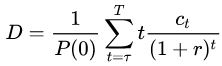
Grazie all’utilizzo di fogli di calcolo (come Excel, per capirci) impostare le formule è più semplice di quanto sembri. In ogni caso non è tanto importante “fare i calcoli” quanto, piuttosto, sapere leggere i risultati.
La duration modificata
Mentre la duration, di per sé, è un indicatore poco utile, la modified duration è di immediata comprensione. Essa, infatti, si determina dividendo la duration per (1+ il rendimento netto del bond) ed esprime il rischio di prezzo di un’obbligazione). In sintesi, la duration modificata ci dice di quanto varia il prezzo tel quel di un bond in seguito ad una variazione dell’1% del suo tasso di rendimento.
A titolo di esempio: una duration modificata di 4 implica che un rialzo dei tassi dell’1% comporterà un ribasso del 4% del prezzo del bond. Viceversa in caso di discesa dei tassi.
Utilizzo pratico dell’indicatore
La durata media finanziaria, scoperta da Macaulay nel 1938, serve a determinare le possibili oscillazioni di un titolo o di un portafoglio di un bond. Si tratta, in altre parole, di un importante indicatore della volatilità di un titolo. Per quanto riguarda i portafogli di obbligazioni, è utile tenere a mente questa informazione. La duration finanziaria di un portafoglio è la media delle duration dei titoli che lo compongono.
Sebbene un investitore prudente faccia bene a contenere la volatilità del proprio portafoglio, un uso speculativo della duration ha le seguenti implicazioni:
- Quando ci si aspetta una salita dei tassi è opportuno ridurre la durata media dei bond. In questo modo si abbatterà anche la volatilità complessiva; In breve, tale obiettivo può essere raggiunto sia attraverso l’investimento in obblgazioni a tasso variabile sia attraverso strumenti derivati a copertura. Grazie a questi è possibile addirittura avere una duration negativa.
- Al contrario, quando ci si aspetta una discesa dei tassi di interesse conviene allungare la durata media del portafoglio. Grazie a questa manovra crescerà anche la duration, con effetti amplificativi sulle quotazioni.
I nostri consigli
Fare trading è il modo sicuro per perdere soldi. Questa regola vale per chi cerca di indovinare il futuro “puntando” sul mercato azionario, sia per l’investitore in bond che cerca di sfruttare l’effetto leva di titoli con scadenza lunga. I mercati tradiscono le aspettative di chi pensa di poterli prevedere. In modo particolare è bene usare le conoscenze acquisite in questo articolo per costruire un portafoglio complessivo efficace tenendo a mente che:
- i bond stabilizzano il portafoglio mentre sono le azioni a dare performance, nel lungo andare;
- durate superiore a 7-10 anni sono sconsigliate per l’investitore fai da te. Esse, in definitiva, imprimono al portafoglio una volatilità eccessiva;
Per questo siamo qui…
Dal 2010 siamo qui per aiutare le persone ad investire diversaMente partendo da ciò che sappiamo di non sapere, e usando un linguaggio semplice, pacato e coinvolgente. Ecco due risorse di approfondimento che ti consigliamo:
- Stai sbagliando approccio con gli investimenti? Scopri come raddrizzare il tiro;
- Leggi le analisi e le ricerche esclusive del nostro Ufficio Studi ogni 7 giorni.
Think different. Invest differently.
Giacomo Saver – CEO di Segreti Bancari








